TAREA EVALUABLE T3
observar los datos y reflexionar acerca de la relación que existe entre las variables calificación, grupo y sexo.
Por simple observación, se puede ver que los estudiantes que utilizan google Apps tienen una calificación superior a los que utilizan moodle. En cuanto a la calificación tomando en consideración el sexo es muy difícil medir a través de la observación.
2- Dibujar en excel o Google Sheets un gráfico de interacción
de las medias de las calificaciones combinando las variables grupo y sexo, es decir: Moodle-Male, Moodle-Female, GoogleApps-Male, GoogleApps-Female. coinciden los resultados mostrados en el gráfico con tus reflexiones del apartado anterior?
Se procede a sacar la media a cada una de las variables combinando el grupo y sexo, obteniéndose los siguientes Datos:
Para sacar la media de los estudiantes de Moodle Masculinos utilice la siguiente formula en Excel.
=PROMEDIO.SI.CONJUNTO (C2:C41, B2:B41,"Moodle", D2:D41,"M")
Para sacar la media de los estudiantes Moodle Femeninos utilice la formula siguiente en Excel.
=PROMEDIO.SI.CONJUNTO (C2:C41, B2:B41,"Moodle", D2:D41,"M")
Para sacar la media de los estudiantes de google Apps Masculino utilice la formula siguiente en Excel.
=PROMEDIO.SI.CONJUNTO (C2:C41, B2:B41,"Google Apps", D2:D41,"M")
Para sacar la media de los estudiantes de google Apps Femenino utilice la formula siguiente en Excel.
=PROMEDIO.SI.CONJUNTO (C2:C41, B2:B41,"Google Apps", D2:D41,"F")
MEDIA POR GRUPO Y POR SEXO
GRÁFICO DE LOS RESULTADOS
Al observar ese gráfico se puede determinar que efectivamente, la media de los estudiantes que utilizan Google Apps, tanto masculino como femenino, es superior a los que utilizan Moodle, lo cual se ajusta a la observación en el paso anterior.
En cuanto al sexo de manera general, se observa que ninguno de los dos presentan los valores más altos, ya que los estudiantes masculino obtuvieron tanto la media más baja (Moodle - Masculino) como la media más alta (Google Apps - Masculino).
En base a los consultados en el material ofrecido por el profesor, se puede determinar que hay interacion , puesto que el efecto de una de las variables independiente depende del nivel de la otra variable independiente. Si observamos en el gráfico, el cambio de plataforma de Moodle a Google Apps si bien aumenta tanto para el caso femenino como para el masculino, está influenciado por el sexo, ya que en un caso aumenta una cantidad considerable y en otro en menor proporción.
Analizar si existen diferencias estadísticamente significativas en las calificaciones en función del grupo y del sexo.
Para realizar este análisis debemos abrir el archivo en R-studio nuestro archivo es notas-2grupo-v3 para luego proceder a dar los pasos de lugar.
Paso 1: Abrimos nuestro archivo que contiene los datos de este ejercicio:
Importar datos: entrar a r-studio clic en importar datos, abrir la carpeta asignaciones finales, seleccionar T2, seleccionar Grupov1 abrir y aparecen los siguientes datos.
Datos a importar
Luego que le damos a importar aparece la pantalla con cuatro columnas las cuales contienen las notas de los estudiantes, tanto Moodle como de google Apps, año y sexo.
Luego que ya tenemos activada la base de datos procedemos a sacar los datos por grupo y sexo.
datos3 <- read.csv("C:/Users/Dell/Desktop/Asignaciones finales/T3/Notas-2grupos-v3.csv", sep=";")
Paso 2: Dividimos nuestros datos en función del grupo y del sexo.
a) Datos en Moddle
datos3Moodle <- subset(datos3, grupo=="Moodle")
b) Datos en Google Apps
datos3GoogleApps <- subset(datos3, grupo=="Google Apps")
c) Datos Masculino
datos3Masculino <- subset(datos3, sexo=="M")
d) Datos Femenino
datos3Femenino <- subset(datos3, sexo=="F")
tabla de los resultados
3: Comparamos los datos para ver si existen
diferencias estadísticas significativas.
Comparación por grupo:
Para lo cual utilizamos el comando siguiente.
t.test(datos3Moodle$nota, datos3GoogleApps$nota)
data: datos3Moodle$nota and datos3GoogleApps$nota
t = -5.6569, df = 38, p-value = 1.683e-06
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.715731 -1.284269
sample estimates:
mean of x mean of y
5.25 7.25
Al analizar los resultados pude ver que hay diferencias
estadísticamente significativas, entre los dos grupos de estudiantes. Porque el margen de error es menor de un cinco por ciento, en virtud de que p-value = 1.683e-06, es decir 0.000001683, lo que equivale a un 0.0001683%.
Comparación por sexo:
Para lo cual utilizamos el siguiente el siguiente comando
t.test(datos3Masculino$nota, datos3Femenino$nota)
Welch Two Sample t-test
data: datos3Masculino$nota and datos3Femenino$nota
t = 0, df = 28.082, p-value = 1
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.982814 0.982814
sample estimates:
Mean of x mean of y
6.25 6.25
En este análisis de los resultados se muestra que por sexo no hubieron diferencias estadísticamente significativas entre los estudiantes. Porque el margen de error es mayor que un cinco por ciento, en virtud de que p-value =1, lo que equivale a un 100%.
4-Utilizar la función aov() de R para saber si existe una interacción estadísticamente significativa entre las variables grupo y sexo.
Para aprender sobre el uso de la función aov() en R, se puede consultar el siguiente documento:
http://courses.statistics.com/software/R/Rtwoway.htm
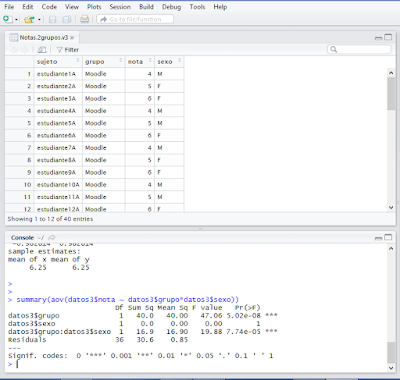
Se utiliza el siguiente comando:
summary(aov(datos3$nota ~ datos3$grupo*datos3$sexo))
Df Sum Sq Mean Sq F value Pr(>F)
datos3$grupo 1 40.0 40.00 47.06 5.02e-08 ***
datos3$sexo 1 0.0 0.00 0.00 1
datos3$grupo:datos3$sexo 1 16.9 16.90 19.88 7.74e-05 ***
Residuals 36 30.6 0.85
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
El análisis de estos resultados muestra que hay una interacción estadísticamente significativa entre las variables grupo y sexo, debido a que el valor de p-value para la interacción es de 7.74e-05, equivalente a 0.0000774, lo que es igual a un 0.00774%.


















0 comentarios:
Publicar un comentario